Садржај

• На корак
• Метод 1 од 3: Први једноставан задатак
• Метод 2 од 3: Израчунавање очекиване вредности за одређени резултат
• Метод 3 од 3: Разумевање концепта
• Савети
• Неопходности

Вредност очекивања је статистички појам и концепт који се користи за одлучивање колико ће нека радња бити корисна или штетна. Да бисте израчунали очекивану вредност, потребно је добро разумети сваки исход у одређеној ситуацији и повезану вероватноћу или вероватноћу да ће се одређени исход догодити. Следећи кораци пружају неке примере вежби које ће вам помоћи да разумете концепт вредности очекивања.

На корак

Метод 1 од 3: Први једноставан задатак

1. Прочитајте изјаву. Пре него што почнете да размишљате о свим могућим исходима и вероватноћама, важно је да разумете проблем. На пример игра коцкама која кошта 10 € по утакмици. Хек коцка се баца једном и ваши добици зависе од броја који баците. Ако се убаци 6, добићете 30 €; 5 зарађује 20 €; било који други број не даје ништа.
2. Наведите све могуће исходе. Помаже у набрајању свих могућих исхода у датој ситуацији. У горњем примеру постоји 6 могућих исхода. То су: (1) баци 1 и изгубиш 10 долара, (2) баци 2 и изгубиш 10 долара, (3) баци 3 и изгубиш 10 долара, (4) баци 4 и изгуби 10 долара , (5) баците петицу и освојите 10 долара, (6) баците 6 и освојите 20 долара.
   • Имајте на уму да је сваки исход за 10 € мањи од горе описаног, јер ћете прво морати да платите 10 € по утакмици, без обзира на исход.
3. Одредите вероватноћу сваког исхода. У овом случају, вероватноћа било којих 6 исхода је иста. Вероватноћа ваљања случајног броја је 1 према 6. Да бисмо то лакше записали, разломак (1/6) ћемо записати у децималу помоћу калкулатора: 0,167. Запишите ову вероватноћу поред сваког исхода, посебно ако желите да решите проблем са различитим вероватноћама за сваки исход.
   • Ваш калкулатор 1/6 може створити нешто попут 0,166667. Заокружујемо ово на 0,167 да бисмо олакшали израчунавање без жртвовања тачности.
   • Ако желите врло тачан резултат, немојте га претварати у децималу, само унесите 1/6 у формулу и израчунајте га на калкулатору.
4. Забележите вредност сваког исхода. Помножите $ резултата са вероватноћом да ће се резултат десити да бисте израчунали колико ће новца тај резултат допринети очекиваној вредности. На пример, резултат котрљања 1 је - 10 УСД, а вероватноћа ваљања 1 је 0,167. Вредност бацања 1 је, према томе, (-10) * (0,167).
   • Нема потребе за израчунавањем ових резултата сада ако имате калкулатор који може истовремено да изводи више операција. Тачнији резултат добићете ако унесете целу једначину.
5. Додајте вредност сваког исхода да бисте добили очекивану вредност догађаја. Да наставимо са горњим примером, вредност очекивања игре коцкицама је: (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (10 * 0,167) + (20 * 0,167), или - 1,67 €. Дакле, можете очекивати да ћете изгубити 1,67 долара сваки пут на овој игри (по утакмици).
6. Какве су импликације израчунавања очекиване вредности. У горњем примеру смо утврдили да би очекивана добит (губитак) била - 1,67 € по бацању. Ово је немогућ исход за 1 утакмицу; можете изгубити 10 €, освојити 10 € или освојити 20 €. Али дугорочно гледано, очекивана вредност је корисна, просечна вероватноћа. Ако наставите да играте ову игру, у просеку ћете изгубити око 1,67 долара по игри. Други начин размишљања о очекиваној вредности је додељивање одређене цене (или користи) игри; ову игру би требали играти само ако сматрате да се исплати, уживајте у њој довољно да сваки пут на њу потрошите 1,67 долара.
   • Што се ситуација чешће понавља, тачније је очекивана вредност приказ стварног, просечног исхода. На пример, можда играте игру 5 пута заредом и сваки пут губите, што резултира просечним губитком од 10 долара. Међутим, ако игру играте још 1000 пута, просечни резултат ће се све више приближавати очекиваној вредности од - 1,67 € по утакмици. Овај принцип назива се „закон великих бројева“.

Метод 2 од 3: Израчунавање очекиване вредности за одређени резултат

1. Користите овај метод за израчунавање просечног броја кованица које треба да преврнете пре него што се појави одређени образац. На пример, методом можете да сазнате очекивани број кованица које ће се окретати док два пута за редом не добијете главе. Овај проблем је мало замршенији од стандардног проблема са вредностима очекивања, па прво прочитајте горњи део овог чланка ако нисте упознати са појмом вредности очекивања.
2. Претпоставимо да тражимо вредност к. Покушавате да утврдите колико кованица у просеку морате да преврнете да бисте добили две главе заредом. Сада правимо поређење да бисмо пронашли одговор. Одговор који тражимо називамо х. Потребно упоређивање вршимо корак по корак. Тренутно имамо следеће:
   • к = ___
3. Размислите шта се дешава ако први флип произведе новчић. То ће бити случај у половини случајева. Ако је то случај, „протратили“ сте превртање, док се шанса да преврнете главом два пута заредом није променила. Као и код бацања новчића, очекује се да морате бацити просечан број пута пре него што двапут заредом добијете главу. Другим речима, очекивали бисте да се окрене к пута више, плус они које сте већ играли. У облику једначине:
   • к = (0,5) (к + 1) + ___
   • Исправићемо празан простор док наставимо да размишљамо о другим ситуацијама.
   • Можете користити разломке уместо децимала ако је то лакше или потребно.
4. Размислите о томе шта се дешава када баците главу. Постоји 0,5 (или 1/2) шансе да први пут баците шољу. Чини се да се ово приближава циљу бацања главе два пута заредом, али колико? Најлакши начин да то сазнате је да размислите о својим могућностима на другом колу:
   • Ако је друго бацање новчић, вратили смо се на почетак.
   • Ако је и други пут шоља, онда смо готови!
5. Научите како да израчунате вероватноћу да се оба догађаја догоде. Сада знамо да имате 50% шансе да баците шољу, али колика је шанса да ћете шољу бацити два пута заредом? Да бисте израчунали ову вероватноћу, помножите вероватноћу обе. У овом случају је 0,5 к 0,5 = 0,25. Наравно, ово је и шанса да ћете закотрљати главе, а затим и репове, јер обоје имају шансе да се 0,5 догоди: 0,5 к 0,5 = 0,25.
6. Додајте једначини резултат за „главе, па репови“. Сада када смо израчунали вероватноћу да се догоди овај догађај, можемо прећи на проширење једначине. Постоји 0,25 (или 1/4) шансе да ћемо бацити бацање два пута без померања напред. Али сада нам још увек треба к више бацања у просеку да бисмо добили резултат који желимо да добијемо, плус 2 која смо већ бацили. У облику једначине ово постаје (0,25) (к + 2), што сада можемо додати једначини:
   • к = (0,5) (к + 1) + (0,25) (к + 2) + ___
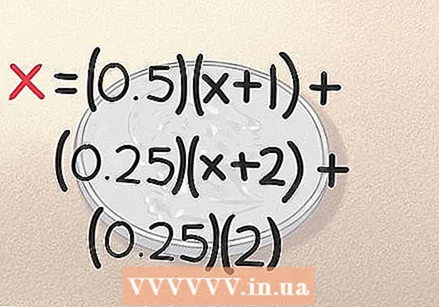7. Додајте једначини резултат за „хеадинг, хеадинг“. Ако се окренете главом, главом са прва два бацања новчића, готови сте. Резултат сте добили за тачно 2 бацања. Као што смо раније приметили, постоји 0,25 шансе да се то догоди, па је једначина за то (0,25) (2). Наше поређење је сада завршено:
   • к = (0,5) (к + 1) + (0,25) (к + 2) + (0,25) (2)
   • Ако нисте сигурни да сте размислили о свакој могућој ситуацији, постоји једноставан начин да проверите да ли је једначина потпуна. Први број у сваком делу једначине представља вероватноћу да ће се догодити неки догађај. То ће увек додати 1. Овде је 0,5 + 0,25 + 0,25 = 1, тако да знамо да смо укључили сваку ситуацију.
8. Поједноставите једначину. Олакшајмо једнаџбу множењем. Запамтите, ако видите нешто у заградама попут ове: (0,5) (к + 1), тада множите 0,5 са сваким појмом који се налази у другом скупу заграда. То вам даје следеће: 0,5к + (0,5) (1) или 0,5к + 0,5. Урадимо то за сваки члан у једначини, а затим комбинујмо ове појмове тако да све изгледа мало једноставније:
   • к = 0,5к + (0,5) (1) + 0,25к + (0,25) (2) + (0,25) (2)
   • к = 0,5к + 0,5 + 0,25к + 0,5 + 0,5
   • к = 0,75к + 1,5
9. Решити за к. Као у било којој једначини, мораћете да изолујете к на једној страни једначине да бисте је израчунали. Запамтите, к значи „просечан број новчића које требате бацити да бисте добили главе два пута заредом“. Када смо израчунали к, пронашли смо и свој одговор.
   • к = 0,75к + 1,5
   • к - 0,75к = 0,75к + 1,5 - 0,75к
   • 0,25к = 1,5
   • (0,25к) / (0,25) = (1,5) / (0,25)
   • к = 6
   • У просеку ћете морати бацити новчић 6 пута пре него што двапут баците главе.

Метод 3 од 3: Разумевање концепта

1. Шта је заправо очекивана вредност. Вредност очекивања није нужно најочигледнији или логичан резултат. Понекад вредност очекивања може бити чак и немогућа вредност у датој ситуацији. На пример, вредност очекивања може бити + 5 € за игру са наградом која не прелази 10 €. Оно што вредност очекивања указује је колико вредност има одређени догађај. Ако игра има очекивану вредност + 5 €, тада је можете играти ако сматрате да вреди времена и новца који можете добити по утакмици. Ако друга игра има очекивану вредност од - 20 УСД, тада је играте само ако мислите да свака игра вреди 20 УСД.
2. Разумевање концепта независних догађаја. У свакодневном животу многи од нас мисле да имамо сретан дан када се догоде неке добре ствари и очекујемо да ће остатак дана ићи тим путем.На исти начин можемо мислити да нам је доста незгоде и да сада заиста треба учинити нешто забавно. Математички, ствари не иду тако. Ако баците обичан новчић, постоји потпуно иста шанса да ћете бацити главу или новчић. Није важно колико сте пута већ бацили; следећи пут када баците и даље ради на исти начин. Бацање новчића је „независно“ од осталих бацања, то на њега не утиче.
   • Уверење да можете имати среће или несреће приликом бацања новчића (или било које друге игре на срећу), или Чињеница да је сва ваша лоша срећа сада завршена и срећа је на вашој страни такође се назива варање коцкара (или заблуда коцкара). То има везе са тенденцијом људи да доносе ризичне или глупе одлуке када осећају да је срећа на њиховој страни или ако осећају „срећни низ“ или ако осећају да ће се „срећа ускоро окренути“.
3. Разумети закон великих бројева. Могли бисте помислити да вредност очекивања није стварно корисна, јер вам само ретко говори какав је стварни исход ситуације. Ако сте израчунали да је очекивана вредност игре рулета - 1 €, а игру играте 3 пута, обично ћете добити - 10 € или + 60 € или неки други резултат. „Закон великих бројева“ помаже да се објасни зашто је вредност очекивања кориснија него што мислите: што више играте, просечни резултат ће бити ближи вредности очекивања. Када погледате велики број догађаја, велике су шансе да је коначни резултат близу очекиване вредности.

Савети

• У оним ситуацијама када су могући вишеструки исходи, на рачунару можете да направите прорачунску табелу за израчунавање очекиване вредности користећи исходе и њихове вероватноће.
• Горњи израчуни за € такође раде у другим валутама.

Неопходности

• Оловка
• Папир
• Калкулатор