Садржај

• Кораци

Тригонометријска једначина садржи једну или више тригонометријских функција променљиве "к" (или било које друге променљиве). Решавање тригонометријске једначине је проналажење такве вредности "к" која задовољава функцију (функције) и једначину у целини.

• Решења тригонометријских једначина изражена су у степенима или радијанима. Примери:

к = π / 3; к = 5π / 6; к = 3π / 2; к = 45 степени; к = 37,12 степени; к = 178,37 степени.

• Напомена: вредности тригонометријских функција из углова, изражене у радијанима, и из углова, изражене у степенима, су једнаке. Тригонометријски круг са радијусом једнаким користи се за описивање тригонометријских функција, као и за проверу исправности решења основних тригонометријских једначина и неједначина.
• Примери тригонометријских једначина:
  • син к + син 2к = 1/2; тг к + цтг к = 1,732;
  • цос 3к + син 2к = цос к; 2син 2к + цос к = 1.

1. Тригонометријски круг полупречника један (јединични круг).
   • То је круг чији је полупречник једнак један и центар у тачки О. Јединични круг описује 4 основне тригонометријске функције променљиве "к", где је "к" угао мерен од позитивног смера осе Кс у смеру супротном од казаљке на сату.
   • Ако је "к" неки угао на јединичној кружници, тада:
   • Хоризонтална оса ОАк дефинише функцију Ф (к) = цос к.
   • Вертикална оса ОБи дефинише функцију Ф (к) = син к.
   • Вертикална оса АТ дефинише функцију Ф (к) = тан к.
   • Хоризонтална оса БУ дефинише функцију Ф (к) = цтг к.

• Јединични круг се такође користи за решавање основних тригонометријских једначина и неједначина (на њему се разматрају различити положаји „к“).

Кораци

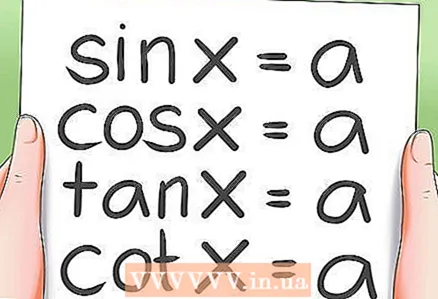1. 1 Концепт решавања тригонометријских једначина.
   • Да бисте решили тригонометријску једначину, претворите је у једну или више основних тригонометријских једначина. Решавање тригонометријске једначине на крају се своди на решавање четири основне тригонометријске једначине.
2. 2 Решавање основних тригонометријских једначина.
   • Постоје 4 врсте основних тригонометријских једначина:
   • син к = а; цос к = а
   • тг к = а; цтг к = а
   • Решавање основних тригонометријских једначина укључује гледање различитих к позиција на јединичном кругу и коришћење табеле за конверзију (или калкулатора).
   • Пример 1.син к = 0.866. Помоћу табеле за конверзију (или калкулатора) добијате одговор: к = π / 3. Јединични круг даје други одговор: 2π / 3. Запамтите: све тригонометријске функције су периодичне, односно њихове вредности се понављају. На пример, периодичност син к и цос к је 2πн, а периодичност тг к и цтг к је πн. Стога је одговор написан на следећи начин:
   • к1 = π / 3 + 2πн; к2 = 2π / 3 + 2πн.
   • Пример 2.цос к = -1/2. Помоћу табеле за конверзију (или калкулатора) добијате одговор: к = 2π / 3. Јединични круг даје други одговор: -2π / 3.
   • к1 = 2π / 3 + 2π; к2 = -2π / 3 + 2π.
   • Пример 3.тг (к - π / 4) = 0.
   • Одговор: к = π / 4 + πн.
   • Пример 4. цтг 2к = 1.732.
   • Одговор: к = π / 12 + πн.
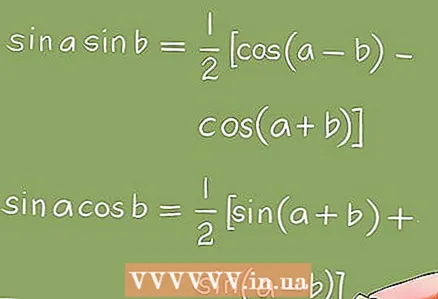3. 3 Трансформације које се користе за решавање тригонометријских једначина.
   • За трансформацију тригонометријских једначина користе се алгебарске трансформације (факторизација, редукција хомогених чланова итд.) И тригонометријски идентитети.
   • Пример 5. Користећи тригонометријске идентитете, једначина син к + син 2к + син 3к = 0 се трансформише у једначину 4цос к * син (3к / 2) * цос (к / 2) = 0. Дакле, потребно је да реши следеће основне тригонометријске једначине: цос к = 0; син (3к / 2) = 0; цос (к / 2) = 0.
     
     
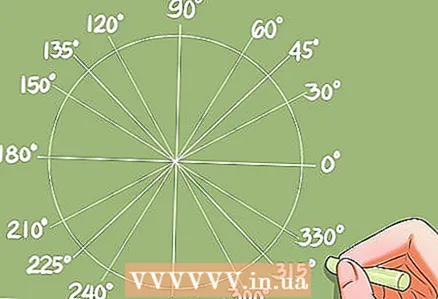
4. 4 Налажење углова из познатих вредности функција.
   • Пре него што научите методе решавања тригонометријских једначина, морате научити како да пронађете углове из познатих вредности функција. То се може урадити помоћу табеле за конверзију или калкулатора.
   • Пример: цос к = 0,732. Калкулатор ће дати одговор к = 42,95 степени. Јединични круг ће дати додатне углове, чији је косинус такође 0,732.
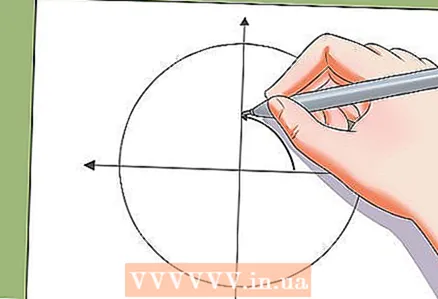5. 5 Оставите раствор на страну јединичног круга.
   • Решења тригонометријске једначине можете одложити на јединичној кружници. Решења тригонометријске једначине на јединичној кружници су темена правилног многоугла.
   • Пример: Решења к = π / 3 + πн / 2 на јединичној кружници су темена квадрата.
   • Пример: Решења к = π / 4 + πн / 3 на јединичној кружници представљају темена правилног шестоугла.
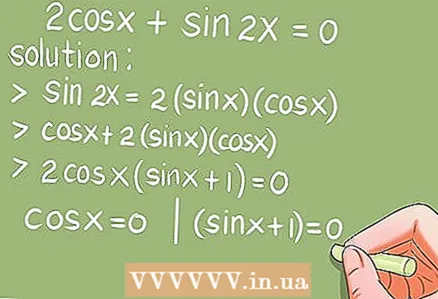6. 6 Методе решавања тригонометријских једначина.
   • Ако дата једначина триг садржи само једну функцију триг, решите ту једначину као основну једначину триг.Ако дата једначина укључује две или више тригонометријских функција, онда постоје 2 методе за решавање такве једначине (у зависности од могућности њене трансформације).
     • Метода 1.
   • Претворите ову једначину у једначину облика: ф (к) * г (к) * х (к) = 0, где су ф (к), г (к), х (к) основне тригонометријске једначине.
     
     
   • Пример 6.2цос к + син 2к = 0. (0 к 2π)
   • Решење. Користећи формулу двоструког угла син 2к = 2 * син к * цос к, замените син 2к.
   • 2цос к + 2 * син к * цос к = 2цос к * (син к + 1) = 0. Сада решите две основне тригонометријске једначине: цос к = 0 и (син к + 1) = 0.
   • Пример 7.цос к + цос 2к + цос 3к = 0. (0 к 2π)
   • Решење: Користећи тригонометријске идентитете, трансформишите ову једначину у једначину облика: цос 2к (2цос к + 1) = 0. Сада решите две основне тригонометријске једначине: цос 2к = 0 и (2цос к + 1) = 0.
   • Пример 8.син к - син 3к = цос 2к. (0 к 2π)
   • Решење: Користећи тригонометријске идентитете, трансформишите ову једначину у једначину облика: -цос 2к * (2син к + 1) = 0. Сада решите две основне тригонометријске једначине: цос 2к = 0 и (2син к + 1) = 0.
     • Метода 2.
   • Претворите дату тригонометријску једначину у једначину која садржи само једну тригонометријску функцију. Затим замените ову тригонометријску функцију неком непознатом, на пример, т (син к = т; цос к = т; цос 2к = т, тг к = т; тг (к / 2) = т, итд.).
   • Пример 9.3син ^ 2 к - 2цос ^ 2 к = 4син к + 7 (0 к 2π).
   • Решење. У овој једначини, замените (цос ^ 2 к) са (1 - син ^ 2 к) (по идентитету). Трансформисана једначина је:
   • 3син ^ 2 к - 2 + 2син ^ 2 к - 4син к - 7 = 0. Замени син к са т. Једначина сада изгледа овако: 5т ^ 2 - 4т - 9 = 0. Ово је квадратна једначина са два корена: т1 = -1 и т2 = 9/5. Други корен т2 не задовољава опсег вредности функције (-1 син к 1). Сада одлучите: т = син к = -1; к = 3π / 2.
   • Пример 10.тг к + 2 тг ^ 2 к = цтг к + 2
   • Решење. Замените тг к са т. Препишите оригиналну једначину на следећи начин: (2т + 1) (т ^ 2 - 1) = 0. Сада пронађите т, а затим к за т = тг к.
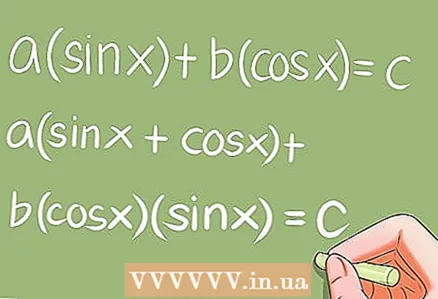7. 7 Посебне тригонометријске једначине.
   • Постоји неколико посебних тригонометријских једначина које захтевају одређене трансформације. Примери:
   • а * син к + б * цос к = ц; а (син к + цос к) + б * цос к * син к = ц;
   • а * син ^ 2 к + б * син к * цос к + ц * цос ^ 2 к = 0
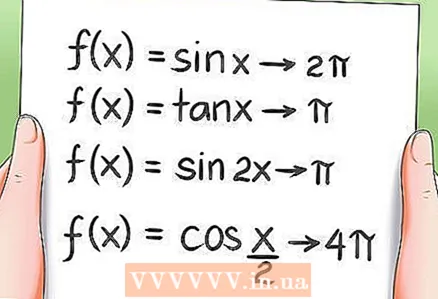8. 8 Периодичност тригонометријских функција.
   • Као што је раније поменуто, све тригонометријске функције су периодичне, односно њихове вредности се понављају након одређеног периода. Примери:
     • Период функције ф (к) = син к је 2π.
     • Период функције ф (к) = тан к једнак је π.
     • Период функције ф (к) = син 2к је π.
     • Период функције ф (к) = цос (к / 2) је 4π.
   • Ако је период наведен у проблему, израчунајте вредност "к" унутар тог периода.
   • Напомена: Решавање тригонометријских једначина није лак задатак и често доводи до грешака. Зато пажљиво проверите своје одговоре. Да бисте то урадили, помоћу графичког калкулатора можете исцртати дату једначину Р (к) = 0. У таквим случајевима решења ће бити представљена као децимални разломци (то јест, π се замењује са 3.14).