Садржај

• Кораци
• Метода 1 од 3: Како решити кубну једначину без сталног члана
• Метода 2 од 3: Како пронаћи целе корене помоћу множитеља
• Метода 3 од 3: Како решити једначину помоћу дискриминатора

У кубичној једначини највећи експонент је 3, таква једначина има 3 корена (решења) и има облик ${ дисплаистиле ак ^ {3} + бк ^ {2} + цк + д = 0}$... Неке кубичне једначине није тако лако решити, али ако примените праву методу (са добром теоријском подлогом), можете пронаћи корене чак и најсложеније кубне једначине - за то користите формулу за решавање квадратне једначине, целе корене или израчунајте дискриминацију.

Кораци

Метода 1 од 3: Како решити кубну једначину без сталног члана

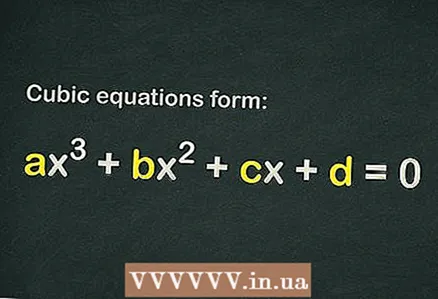1. 1 Сазнајте има ли слободног члана у кубној једначини д{ дисплаистиле д}. Кубична једначина има облик ${ дисплаистиле ак ^ {3} + бк ^ {2} + цк + д = 0}$... Да би се једначина сматрала кубичном, довољно је да се само израз ${ дисплаистиле к ^ {3}}$ (то јест, можда уопште нема других чланова).
   • Ако једначина има слободан члан ${ дисплаистиле д}$, користите другу методу.
   • Ако је у једначини ${ дисплаистиле а = 0}$, није кубична.
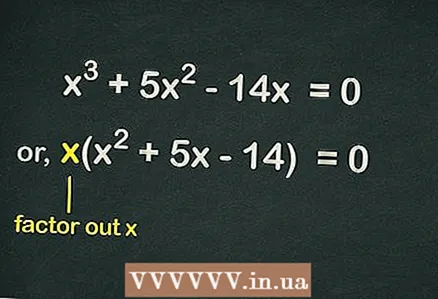2. 2 Извадите из заграда Икс{ дисплаистиле к}. Пошто у једначини нема слободног члана, сваки члан у једначини укључује променљиву ${ дисплаистиле к}$... То значи тај ${ дисплаистиле к}$ могу се искључити из заграда ради поједностављења једначине. Тако ће једначина бити написана овако: ${ дисплаистиле к (секира ^ {2} + бк + ц)}$.
   • На пример, с обзиром на кубну једначину ${ дисплаистиле 3к ^ {3} -2к ^ {2} + 14к = 0}$
   • Извадити ${ дисплаистиле к}$ заграде и добити ${ дисплаистиле к (3к ^ {2} -2к + 14) = 0}$
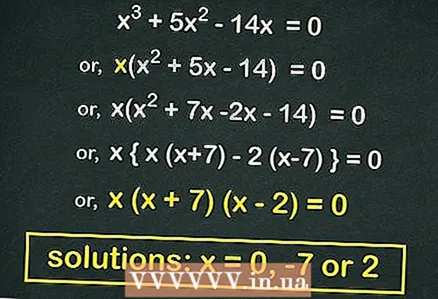3. 3 Фактор (производ два бинома) квадратну једначину (ако је могуће). Многе квадратне једначине облика ${ дисплаистиле секира ^ {2} + бк + ц = 0}$ може се факторисати. Таква једначина ће се испоставити ако је извадимо ${ дисплаистиле к}$ изван заграда. У нашем примеру:
   • Извадите из заграда ${ дисплаистиле к}$: ${ дисплаистиле к (к ^ {2} + 5к-14) = 0}$
   • Фактор квадратне једначине: ${ дисплаистиле к (к + 7) (к-2) = 0}$
   • Изједначите сваку канту на ${ дисплаистиле 0}$... Корени ове једначине су ${ дисплаистиле к = 0, к = -7, к = 2}$.
4. 4 Решите квадратну једначину помоћу посебне формуле. Учините то ако се квадратна једначина не може факторисати. Да би се пронашли два корена једначине, вредности коефицијената ${ дисплаистиле а}$, ${ дисплаистиле б}$, ${ дисплаистиле ц}$ замена у формули ${ дисплаистиле { фрац {-б пм { скрт {б ^ {2} -4ац}}} {2а}}}$.
   • У нашем примеру, замените вредности коефицијената ${ дисплаистиле а}$, ${ дисплаистиле б}$, ${ дисплаистиле ц}$ (${ дисплаистиле 3}$, ${ дисплаистиле -2}$, ${ дисплаистиле 14}$) у формулу:

     ${ дисплаистиле { фрац {-б пм { скрт {б ^ {2} -4ац}}} {2а}}}$

     ${ дисплаистиле { фрац {- (- 2) пм { скрт {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ дисплаистиле { фрац {2 пм { скрт {4- (12) (14)}}} {6}}}$

     ${ дисплаистиле { фрац {2 пм { скрт {(4-168}}} {6}}}$

     ${ дисплаистиле { фрац {2 пм { скрт {-164}}} {6}}}$

   • Први корен:

     ${ дисплаистиле { фрац {2 + { скрт {-164}}} {6}}}$

     ${ дисплаистиле { фрац {2 + 12,8и} {6}}}$

   • Други корен:

     ${ дисплаистиле { фрац {2-12,8и} {6}}}$

5. 5 Користите нула и квадратне корене као решења кубичне једначине. Квадратне једначине имају два корена, док кубичне имају три. Већ сте пронашли два решења - ово су корени квадратне једначине. Ако ставите "к" изван заграда, треће решење би било ${ дисплаистиле 0}$.
   • Ако из заграда извадите „к“, добићете ${ дисплаистиле к (секира ^ {2} + бк + ц) = 0}$односно два фактора: ${ дисплаистиле к}$ и квадратну једначину у загради. Ако је било који од ових фактора ${ дисплаистиле 0}$, цела једначина је такође једнака ${ дисплаистиле 0}$.
   • Дакле, два корена квадратне једначине су решења кубне једначине. Треће решење је ${ дисплаистиле к = 0}$.

Метода 2 од 3: Како пронаћи целе корене помоћу множитеља

1. 1 Уверите се да у кубној једначини постоји слободан израз д{ дисплаистиле д}. Ако се у једначини облика ${ дисплаистиле ак ^ {3} + бк ^ {2} + цк + д = 0}$ постоји слободан члан ${ дисплаистиле д}$ (што није једнако нули), неће бити могуће ставити „к“ изван заграда. У овом случају користите метод описан у овом одељку.
   • На пример, с обзиром на кубну једначину ${ дисплаистиле 2к ^ {3} + 9к ^ {2} + 13к = -6}$... Да бисте добили нулу на десној страни једначине, додајте ${ дисплаистиле 6}$ на обе стране једначине.
   • Једначина ће се испоставити ${ дисплаистиле 2к ^ {3} + 9к ^ {2} + 13к + 6 = 0}$... Као ${ дисплаистиле д = 6}$, метода описана у првом одељку не може се користити.
2. 2 Запишите факторе коефицијента а{ дисплаистиле а} и слободан члан д{ дисплаистиле д}. То јест, пронађите факторе броја на ${ дисплаистиле к ^ {3}}$ и бројеве испред знака једнакости. Подсетимо се да су чиниоци броја бројеви који, када се помноже, производе тај број.
   • На пример, да бисте добили број 6, потребно је да се множи ${ дисплаистиле 6 пута 1}$ и ${ дисплаистиле 2 пута 3}$... Дакле, бројеви 1, 2, 3, 6 су фактори броја 6.
   • У нашој једначини ${ дисплаистиле а = 2}$ и ${ дисплаистиле д = 6}$... Множитељи 2 су 1 и 2... Множитељи 6 су бројеви 1, 2, 3 и 6.
3. 3 Поделите сваки фактор а{ дисплаистиле а} за сваки фактор д{ дисплаистиле д}. Као резултат тога, добијате много разломака и неколико целих бројева; корени кубичне једначине биће један од целих бројева или негативна вредност једног од целих бројева.
   • У нашем примеру поделимо факторе ${ дисплаистиле а}$ (1 и 2) по факторима ${ дисплаистиле д}$ (1, 2, 3 и 6). Добићете: ${ дисплаистиле 1}$, ${ дисплаистиле { фрац {1} {2}}}$, ${ дисплаистиле { фрац {1} {3}}}$, ${ дисплаистиле { фрац {1} {6}}}$, ${ дисплаистиле 2}$ и ${ дисплаистиле { фрац {2} {3}}}$... Сада овој листи додајте негативне вредности добијених разломака и бројева: ${ дисплаистиле 1}$, ${ дисплаистиле -1}$, ${ дисплаистиле { фрац {1} {2}}}$, ${ дисплаистиле - { фрац {1} {2}}}$, ${ дисплаистиле { фрац {1} {3}}}$, ${ дисплаистиле - { фрац {1} {3}}}$, ${ дисплаистиле { фрац {1} {6}}}$, ${ дисплаистиле - { фрац {1} {6}}}$, ${ дисплаистиле 2}$, ${ дисплаистиле -2}$, ${ дисплаистиле { фрац {2} {3}}}$ и ${ дисплаистиле - { фрац {2} {3}}}$... Цео корен кубичне једначине су неки бројеви са ове листе.
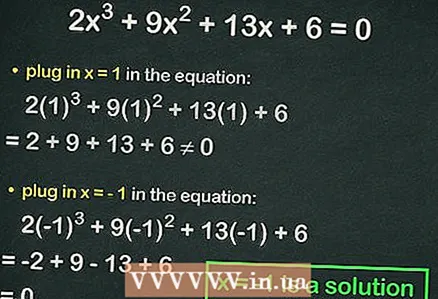4. 4 Укључите целе бројеве у кубну једначину. Ако је једнакост тачна, замењени број је корен једначине. На пример, замените у једначини ${ дисплаистиле 1}$:
   • ${ дисплаистиле 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ дисплаистиле 2 + 9 + 13 + 6}$ = 0, односно једнакост се не поштује. У том случају прикључите следећи број.
   • Замена ${ дисплаистиле -1}$: ${ дисплаистиле (-2) +9 +(- 13) +6}$ = 0. Дакле, ${ дисплаистиле -1}$ је цео корен једначине.
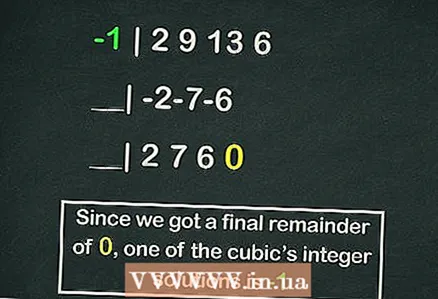5. 5 Користите метод дељења полинома са Хорнерова шемакако би брже пронашли корене једначине. Учините то ако не желите да ручно замените бројеве у једначину. У Хорнеровој шеми, цели бројеви су подељени вредностима коефицијената једначине ${ дисплаистиле а}$, ${ дисплаистиле б}$, ${ дисплаистиле ц}$ и ${ дисплаистиле д}$... Ако су бројеви равномерно дељиви (то јест, остатак је ${ дисплаистиле 0}$), цео број је корен једначине.
   • Хорнерова шема заслужује посебан чланак, али следећи је пример израчунавања једног од корена наше кубне једначине помоћу ове шеме:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Дакле, остатак је ${ дисплаистиле 0}$, али ${ дисплаистиле -1}$ је један од корена једначине.

Метода 3 од 3: Како решити једначину помоћу дискриминатора

1. 1 Запишите вредности коефицијената једначине а{ дисплаистиле а}, б{ дисплаистиле б}, ц{ дисплаистиле ц} и д{ дисплаистиле д}. Препоручујемо да унапред запишете вредности наведених коефицијената како се не бисте збунили у будућности.
   • На пример, с обзиром на једначину ${ дисплаистиле к ^ {3} -3к ^ {2} + 3к -1}$... Записати ${ дисплаистиле а = 1}$, ${ дисплаистиле б = -3}$, ${ дисплаистиле ц = 3}$ и ${ дисплаистиле д = -1}$... Подсјетимо се да је прије ${ дисплаистиле к}$ нема броја, одговарајући коефицијент и даље постоји и једнак је ${ дисплаистиле 1}$.
2. 2 Израчунајте нулти дискриминатор користећи посебну формулу. Да бисте решили кубну једначину помоћу дискриминатора, потребно је да изведете низ тешких прорачуна, али ако све кораке изведете исправно, ова метода ће постати неопходна за решавање најсложенијих кубних једначина. Прво рачунање ${ дисплаистиле Делта _ {0}}$ (нула дискриминатора) је прва вредност која нам је потребна; да бисте то урадили, замените одговарајуће вредности у формули ${ дисплаистиле Делта _ {0} = б ^ {2} -3ац}$.
   • Дискриминант је број који карактерише корене полинома (на пример, дискриминатор квадратне једначине се израчунава формулом ${ дисплаистиле б ^ {2} -4ац}$).
   • У нашој једначини:

     ${ дисплаистиле б ^ {2} -3ац}$

     ${ дисплаистиле (-3) ^ {2} -3 (1) (3)}$

     ${ дисплаистиле 9-3 (1) (3)}$

     ${ дисплаистиле 9-9 = 0 = Делта _ {0}}$

3. 3 Израчунајте први дискриминатор користећи формулу Δ1=2б3−9абц+27а2д{ дисплаистиле Делта _ {1} = 2б ^ {3} -9абц + 27а ^ {2} д}. Први дискриминатор ${ дисплаистиле Делта _ {1}}$ - ово је друга важна вредност; да бисте га израчунали, укључите одговарајуће вредности у наведену формулу.
   • У нашој једначини:

     ${ дисплаистиле 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ дисплаистиле 2 (-27) -9 (-9) +27 (-1)}$

     ${ дисплаистиле -54 + 81-27}$

     ${ дисплаистиле 81-81 = 0 = Делта _ {1}}$

4. 4 Израчунај:${ дисплаистиле Делта = ( Делта _ {1} ^ {2} -4 Делта _ {0} ^ {3}) див -27а ^ {2}}$... Односно, кроз добијене вредности пронађите дискриминатор кубне једначине ${ дисплаистиле Делта _ {0}}$ и ${ дисплаистиле Делта _ {1}}$... Ако је дискриминатор кубичне једначине позитиван, једначина има три корена; ако је дискриминатор нула, једначина има један или два корена; ако је дискриминатор негативан, једначина има један корен.
   • Кубична једначина увек има најмање један корен, будући да граф ове једначине пресеца осу Кс најмање у једној тачки.
   • У нашој једначини ${ дисплаистиле Делта _ {0}}$ и ${ дисплаистиле Делта _ {1}}$ једнаки ${ дисплаистиле 0}$, тако да можете лако израчунати ${ дисплаистиле Делта}$:

     ${ дисплаистиле ( Делта _ {1} ^ {2} -4 Делта _ {0} ^ {3}) див (-27а ^ {2})}$

     ${ дисплаистиле ((0) ^ {2} -4 (0) ^ {3}) див (-27 (1) ^ {2})}$

     ${ дисплаистиле 0-0 див 27}$

     ${ дисплаистиле 0 = Делта}$... Дакле, наша једначина има један или два корена.

5. 5 Израчунај:${ дисплаистиле Ц = ^ {3} { скрт { лефт ({ скрт { Делта _ {1} ^ {2} -4 Делта _ {0} ^ {3}}} + Делта _ {1 } десно) див 2}}}$. ${ дисплаистиле Ц}$ - ово је последња важна количина која се може пронаћи; то ће вам помоћи да израчунате корене једначине. Замените вредности наведеном формулом ${ дисплаистиле Делта _ {1}}$ и ${ дисплаистиле Делта _ {0}}$.
   • У нашој једначини:

     ${ дисплаистиле ^ {3} { скрт {{ скрт {( Делта _ {1} ^ {2} -4 Делта _ {0} ^ {3}) + Делта _ {1}}} див 2}}}$

     ${ дисплаистиле ^ {3} { скрт {{ скрт {(0 ^ {2} -4 (0) ^ {3}) + (0)}} див 2}}}$

     ${ дисплаистиле ^ {3} { скрт {{ скрт {(0-0) +0}} див 2}}}$

     ${ дисплаистиле 0 = Ц}$

6. 6 Пронађи три корена једначине. Урадите то са формулом ${ дисплаистиле - (б + у ^ {н} Ц + Делта _ {0} див (у ^ {н} Ц)) див 3а}$, где ${ дисплаистиле у = (- 1 + { скрт {-3}}) див 2}$, али н је једнако 1, 2 или 3... Замените одговарајуће вредности овом формулом - као резултат ћете добити три корена једначине.
   • Израчунајте вредност користећи формулу на н = 1, 2 или 3а затим проверите одговор. Ако добијете 0 када проверите одговор, ова вредност је корен једначине.
   • У нашем примеру, замена 1 у ${ дисплаистиле к ^ {3} -3к ^ {2} + 3к -1}$ и добити 0, тј 1 је један од корена једначине.